Demo
Tutorial
A simple example
Type 1⏎-x⏎frac⏎ (⏎ denotes enter key) into the textbox above. You will get \(\small\displaystyle\frac{1}{-x}\) in Level1 of the stack.
Note that the editing operator (frac) and the operands (1 and -x) are entered one by one.
Continue typing as 3⏎-⏎ and now you have \(\small\displaystyle\frac{1}{-x}-3\) in Level 1.
Tick the "Source" button just under the textbox (or type pop⏎) to get the LaTeX source: \frac{1}{-x}-3.
The rule of this processing is simple:
(1) Any editing operator or operand you've entered in the textbox is pushed to the stack.
(2) If what you've entered is an editing operator, it works immediately to consume a certain number of operands and to push the result into the stack.
(3) Go to (1).
All operations are done on your computer and no information is sent to the outside of your browser except that MathJax is used to preview.
Learn more
- Many editing operators have the same names as LaTeX commands without \. For example, div operator consumes two operands from the stack and joins them with ÷ (which is \div in the source code). Have a try at times, +, -, ^, _ (these consume two operands), sin, int, and sqrt(these consume one).
- Use a double quotation mark to escape the name of an editing operator. For example "div for div.
- There are some editing operators outside the LaTeX context. For example, join operator consumes two operands from the stack and literaly joins them literally; () operator puts "(" and ")" before and after the operand; leftright operator make a pair of parentheses larger to make them fit their contents.
- Some editing operators can have integers just after them to control the behaviour of themselves. For example, join3 joins three strings and join5 joins five.
- There are some operators which handle the stack itself. drop, pop, clear, and swap would be the most often used.
- Abbreviations are defined for Greek letters. For example, @d is replaced by δ (\delta in the source) before the string is pushed to the stack. For example, @donkey⏎ produces \(\delta onkey\).
- To produce arrays or matrices we have some editing operators. For example, 1⏎2⏎3⏎4⏎5⏎6⏎array2x3⏎ produces 2x3 array.
- undo cancels the last operation.
Advanced features
- By using sto operator you can assign any text to any name you like. For example, once you type 3.14⏎pi⏎sto⏎, after that you can use pi for 3.14. Your assignments persist through sessions using localStorage of your browser. Any data is not sent to the outside of your computer. To delete the assignment type "pi⏎purge⏎. To delete all the assignments use purgeall.
- Two or more operators or/and operands can be put together in a structure called macro. For example, <<<1%swap%frac>>> is a macro which works the same as 1⏎swap⏎frac⏎ that gives the reciprocal. It's a good idea to assign your macro to a name you like. "<<<1%swap%frac>>>⏎recip⏎sto⏎ will make your recip operator. (Note that " is needed just before the macro to escape it, otherwise it works immediately when it is pushed to the stack.)
- To specify the times of repetition you can add a prefix Ntimes: before operator names. For example, 2times:+⏎ is the equivalent to +⏎+⏎.
Editing operators
Brown letters suggest that the editing operator uses control sequences supported only by AMS LaTeX. Green letters suggest that the editing operator uses control sequences not supported by Plain TeX.
Operators which consume two Levels from the stack
+- changes the sign. ++ changes the sign to +. -- changes the sign to -. pmpm changes the sign to \(\pm\). mpmp changes the sign to \(\mp\).
+ - ^ _ times div ast star circ bullet cdot cap cup uplus sqcap sqcup vee lor wedge land setminus wr diamond bigtriangleup bigtriangledown triangleleft triangleright lhd rhd unlhd unrhd oplus ominus otimes oslash odot bigcirc dagger ddagger amalg
< > = : ne neq le leq ge geq prec preceq ll subset subseteq supset supseteq sqsubset sqsupset sqsubseteq sqsupseteq in ni owns vdash dashv succ succeq gg equiv sim simeq cong asymp approx neq doteq propto models perp mid parallel bowtie Join smile frown
leftarrow rightarrow to leftrightarrow Leftarrow Rightarrow Leftrightarrow longleftarrow longrightarrow longleftrightarrow Longleftarrow Longrightarrow Longleftrightarrow leftharpoonup rightharpoonup rightleftharpoons leftharpoondown rightharpoondown rightharpoondown leftrightharpoons hookleftarrow hookrightarrow mapsto longmapsto leadsto
vert | Vert \| backslash uparrow downarrow updownarrow Uparrow Downarrow Updownarrow
sqrtn gives \(\displaystyle\sqrt[{\rm Level1}]{{\rm Level2}}\)
bigcap bigcup bigsqcup bigvee bigwedge bigodot bigotimes bigoplus biguplus
frac cfrac over atop choose brace brack sqrt
sideset insert \sideset control sequence before the text in Level1. \sideset affects the behaviour of ^, _, left^, and left_.
left^ left_ put Level1 to the upper/down left side of Level2 as a superscript/subscript.
Operators which consume one Level from the stack
sin cos tan sinh cosh tanh csc sec cot coth arcsin arccos arctan exp log ln ker arg deg lg det dim gcd hom max min Pr sum prod coprod int oint lim inf liminf varliminf sup limsup varlimsup projlim injlim varinjlim varprojlim
bigm Bigm biggm Biggm find a delimiter in Level 1 and insert the respective LaTeX control sequence just before it.
() [] \{\} <> .. || |||| You can make an operator choosing opening and closing parenthesis respectively. For example, (| can be an operator which put ( before the text and | after. Also you can use . (period) as both an opening and closing parenthesis.
{} floor ceil //
leftright biglbigr BiglBigr bigglbiggr BigglBiggr When Level 1 have opening and closing parentheses at its both ends, these operators make them larger.
forall exists neg partial angle
' '' hat check breve acute grave tilde bar vec dot ddot
overline underline overrightarrow overleftarrow widehat widetilde overbrace underbrace
bf rm cal sf tt it mathbf mathrm mathcal mathsf mathtt mathit boldsymbol pmb
displaystyle textstyle scriptstyle scriptscriptstyle
mbox text operatorname
mathord mathop mathbin mathrel mathopen mathclose mathpunct mathinner
decapN delete the first N character(s) in Level 1 (default N=1.)
chopN delete the last N character(s) in Level 1 (default N=1.)
$$ \(\) math put the equation in Level 1 in an inline math environment.
$$$$ \[\] displaymath equation* equation put the equation in Level 1 in a display math environment.
shoveright shoveleft put Level 1 into \shoveleft{} or \shoveright{}. They are for multiline mode.
Operators which consume N Levels from the stack
joinN consumes N Levels to join them to produce a string. (default N=2)
joinwithN consumes N+1 Levels to join the texts from Level N+1 to Level 2 using the text in Level 1 as a separator. (default N=2)
toRxC arrayRxC matrixRxC pmatrixRxC bmatrixRxC BmatrixRxC vmatrixRxC VmatrixRxC smallmatrixRxC consume RxC Levels to produce a matrices that have \(R\) rows and \(C\) columns (\(R\) and \(C\) must be integers).
multline*N multlineN consume N Levels to produce an equation by giving it the respective environment. (default N=2)
eqnarray*N eqnarrayN collectN equations from N Levels to put them together in eqnarray environment. Note that these operator don't insert alignment points.(default N=2)
eqalignN collect N equations from N Levels to put them together in \eqalign{ }. This is for Plain TeX only.(default N=2)
eqnarray&*N eqnarray&N are the same as eqnarray*N and eqnarrayN but insert &s before and after = in each Level. (default N=2)
gather*N gatherN collectN equations from N Levels to put them together in gather environment.
splitN split&N The later insetrts alignment points automatically to each equation.
align*RxC alignRxC flalign*RxC flalignRxC collect equations from RxC Levels to make a RxC array and put it in an align environment. Note that these operator don't insert alignment points. Preview doesn't work for flalign*RxC and flalign&RxC in this page.
align*&RxC align&RxC flalign*&RxC flalign&RxC are the same as their without-&-versions except that these operators insert alignment points automatically. Preview doesn't work for flalign&*RxC and flalign&RxC in this page.
Abbreviations
Stack operation
undo cancels the last operation to have the stack revert to the former state.
savestack saves the whole stack as a macro and assigns it to the name "resume". This means that you can resume the saved stack by typing as clear⏎resume⏎.
resume is a reserved name with which the whole stack is saved by savestack operator.
savestackas saves the whole stack except Level 1 as a macro and assigns it to the name held in Level 1.
collectfromMtoN collects the contents from LevelM to N and makes a macro.
dropN drops N levels from level 1 to Level N. (Default N=1.)
pop copy Level 1 to the input box and drop Level 1.
clear drops all levels.
nip drops all levels except Level 1.
swap swaps Level 1 and Level 2.
dupN duplicates the N levels from Level N to Level 1. (Default N=1)
pickN Copies Level N and push it. (Default N=3.)

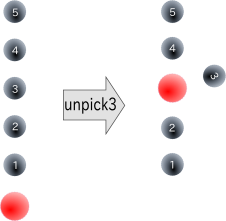
unpickN Drops Level 1 and replace Level N+1 with it. (Default N=3.)
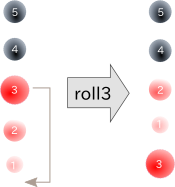
rollN moves what is in level N to Level1, moves what is in Level1 to Level2... ,and moves what is in Level\((N-1)\) to LevelN, in other words it is the cyclic permutation (Level1 Level2 ... LevelN). (Default N=3.)
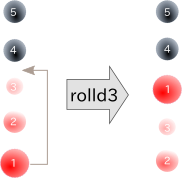
rolldN moves what is in Level1 to LevelN, moves what is in Level2 to Level1,....,and what is in LevelN moves to Level\((N-1)\), in other words it is the cyclic permutation (LevelN LevelN-1 ... Level1).(Default N=3.)
@MAX is replaced by the size of the stack just like an abbreviation. So you can apply an cyclic permutation all over the stack by roll@MAX⏎ or rolld@MAX⏎.
Assignment
sto assign the text in Level2 to the name in Level1.
purge consume Level1 to make the name free.
purgeall delete all assignments.
getdef gets a name from Level 1 and pushes the assigned object.