2015-5-9(Sat)
hp50g はグラフ機能と数式処理機能を備えた高性能な電卓である。高校生のときにこれを持っていたら何ができただろうか?と思っていろいろ遊んでみた。
高校で勉強する公式を、hp50g を使って左辺から右辺、右辺から左辺に変形することができるかどうか、試してみた。

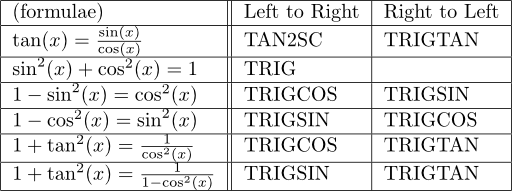
TRIG はピタゴラスの定理(sin^2+cos^2=1)を使った式の変形を行う。マニュアルには、「Converts complex logarithmic and exponential subexpressions into their equivalent trigonometric expressions.」とあるけれども、高校では三角関数と指数・対数関数はぜんぜん別物ということなので、まあそういうことで。
TRIGCOS, TRIGSIN, TRIGTAN はその仲間で、それぞれ cos を優先、sin を優先する。また、TRIGTAN は、tan の定義も使って、tan を優先する。TAN2SC は、tan を定義に従って sin と cos で書き換えるもの。
次が高校数学のメイン・ディッシュのひとつである加法定理。
TEXPAND は、式の展開をしてくれる EXPAND の超越関数版(T というのは、transcendental の頭文字)で、三角関数を含んだ式に使うと加法定理を使ってバラしてくれる。
TCOLLECT の T は trigonometric の T で、加法定理を使って SIN と COS を纏めてくれる。

次は教科書の最初のほうに出てくる話だが、加法定理より後にしたのにはわけがある。ようするに、hp50g はこれらの式を、加法定理を用いて変形するのである。単位円を書いて考えれば当たり前のようなことを、より一般的な見方で処理するのに興がある。
なお、hp50g でこれらの書き換えやろうとすると、左辺から右辺への一方通行になってしまう。一般的に言って、複雑な形を単純な形にすることはできても、単純な形を複雑な形にすることは数式処理機能の範囲外。もっとも、何が単純な形なのかは、なかなか意味深いものだったりする。
EVAL は直訳すると「評価」であるが、数学でいう評価のことではなくて、プログラミング的なそれ。ここでは、ちょいちょいと式を簡単にしてくれる感じ。
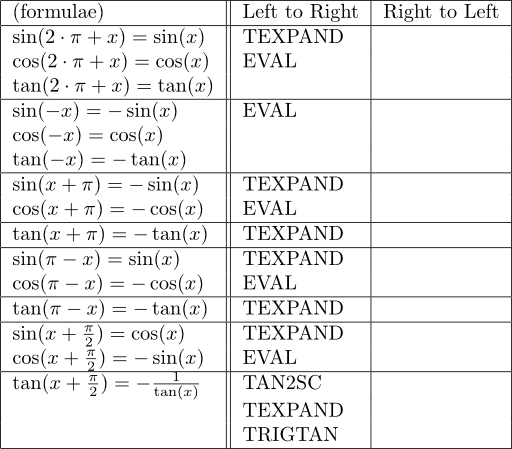
上の表の最後のやつ(tan(x+π/2))だが、いったん TAN2SC で tan を sin と cos に直している。これをやらないで、TEXPAND をやると hp50g は「?」を出してしまう。TEXPAND は tan の加法定理を使おうとするが、途中で tan(π) が出てきて?になってしまうのだと思う。
加法定理から導かれるやつ。

倍角公式の見方を変えたやつ。
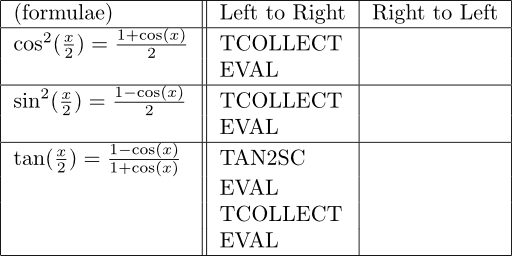
「三角関数の合成」という見出しがついてるやつ。
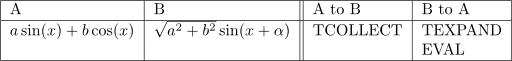
次は、いわゆる積を和にする公式とか、和を積にする公式とか言われているやつ。

まずは指数法則。
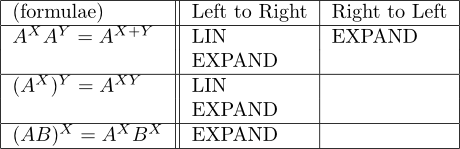
hp50g での対数は、底が e (LN) か 10 (LOG) かしか使えないので、底がこれら以外の場合は、底を e か 10 にしておく必要がある。まあ、ふつうは e がいい※と思うけど。(※駄洒落)
LIN は「Linearizes expressions involving exponential terms.」
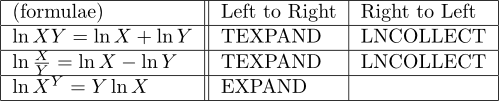
LNCOLLECT は「Simplifies an expression by collecting logarithmic terms.」
おわり